為什麼透視圖的消失點會連成一條消失線?
最近在研究影像處理,在思考照片中的物體,會如何隨著相機拍攝的角度改變而變形。因此產生了一個有趣的疑問:為什麼照片中的透視點能夠連成一條線?
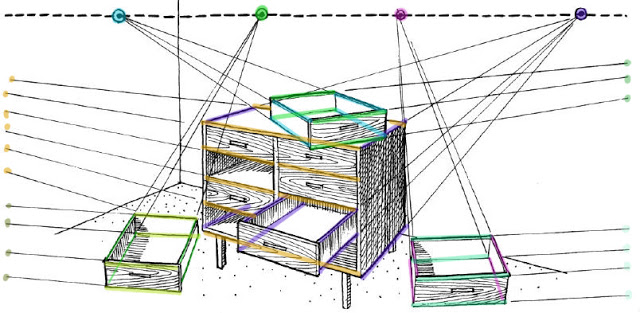
圖片引用自DesignByFoot blog
可以看到上圖中,不論是地上的抽屜、櫃子,只要將平行線的兩端延伸,最後就會交於一點,而這些不同平行線延伸出的交點,最後竟然會交於同一條水平線上,我覺得這實在是太神奇了,不禁好奇為什麼會有這個現象?
這個問題看似簡單,其實並不好思考。我想說學設計的應該會對透視比較了解,所以問了幾位學設計的朋友,他們其實也不太會解釋為什麼,就說是一種FU(馬的到底是什麼FU啦XD),我看了好幾篇文章,有設計的、也有計算機圖學的,平常在走廊走路時像怪人一樣不斷的看天花板無限延伸的平行線發呆,想了幾天,才總算搞懂這是怎麼一回事。
這裡的透視不是透明的意思,而是一種投影的現象。其實你每天張開眼睛,看到的畫面通通都是透視圖。無限延伸的鐵軌會在遠方交於一點是最經典的例子。

這是個很有趣的現象,現在想像假設地面上有不只一條的鐵軌,通通朝正前方延伸,有一個很重要的現象是,這些鐵軌通通會交於一點。
會這樣
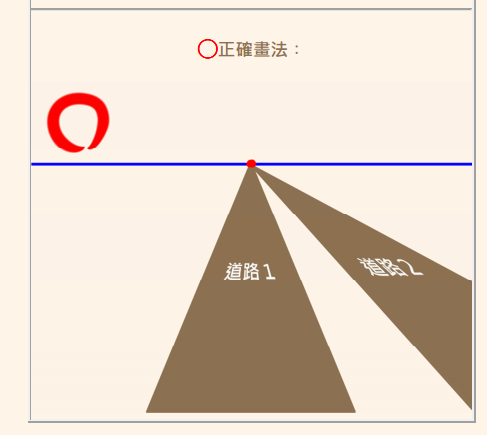
而不會這樣
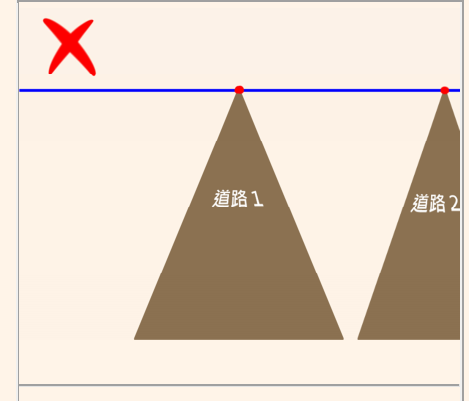
同樣地,如果我們從高空俯視大樓,會發現所有的牆壁邊線無限延伸後,都會交於同一點。
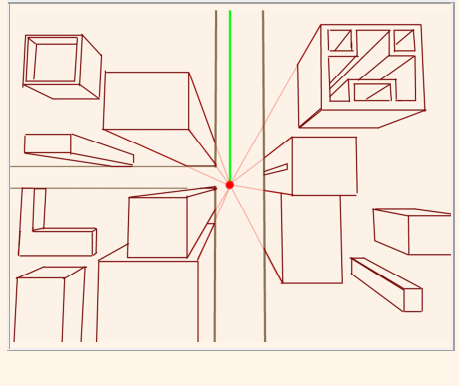
上面這三張圖都出自巴哈姆特 Arrogant(傲慢的羊)寫的透視教學,他的文章是針對繪畫的透視做介紹,是我目前看來最清晰易懂的教學,相當推薦
這個現象很直觀,我們可以從這裡切入,第一個要思考的問題是,為什麼會有這個現象?
攝像機模型
讓我們用更具體的模型來觀察透視現象。
圖片出自the university of edinburgh
所謂的透視,就是將三維世界座標系的物體,投影到某個平面上的現象。可以看到上圖的原點代表投影中心,投影中心前方有一個平面。而所謂的投影,就是將三維世界的物體,和投影中心連成一線,交於該平面上產生的圖樣。

圖片引用自Wiki Vanishing Point
現在我們將剛剛的延伸的鐵路,透過這個攝像機模型來表示,上圖可以看到隨著鐵軌的延伸,遠方的鐵軌和投影中心的連線越來越接近平行地面的直線,最後那個無限遠的點,其實就是一條由投影中心發出,平行於鐵軌方向的直線,交於平面上的點。
推廣到不同角度的鐵軌
現在,想像另一種情況。假設這個鐵軌不是往正前方無限延伸,而是例如朝右45度無限延伸,那麼他會交於圖片上哪一點?

圖都找給你看了,答案很明顯吧。會在偏右的位置。 如果用剛剛所提的,這個點其實會在一條由投影中心發出,平行於該偏右鐵軌的直線,交於平面上的點

自己畫的廢廢手繪圖 注意我講的偏右的意思是,你的視線朝正前方看,此時腳下的鐵軌往右偏。你的視線往前看,但用眼角餘光觀測鐵軌,發現鐵軌的盡頭位於整個視野中偏右的位置。如果你轉個身,讓視線和鐵軌朝同一個方向,那麼鐵軌的無限遠處自然就在視野的正中央了。
現在我們得到一個非常重要,基本上是整個透視投影界(?)最重要的觀念:所有同樣方向平行線的無限遠處,會落在投影平面上的同一點 所有朝正前方平行的鐵軌的無限遠處會落在同一點,所有朝右方45度平行的鐵軌的無限遠處也會落在同一點。而這些點都被叫做消失點,而消失點的座標恰好是一條從投影中心發出,平行於該鐵軌方向的直線,落在投影平面上的點。
為什麼這些透視點會連成一條線
掌握這些觀念後,現在我們要回答本文一開始的問題:為什麼這些透視點會連成一條線? 因為這些不同方向的鐵軌(或物體)都平行於地面,因此從透視中心發出到無限遠處的射線也會平行於地面。他們可能有不同的方向,朝正前方的鐵軌的消失點在正前方,偏右的鐵軌消失點在偏右的地方,但是無論是哪個方向的鐵軌,從透視中心延伸到投影平面上消失點的射線都平行於地面,因此他們都在同一個高度上,成為一條由消失點構成的水平線。

看看一開始的圖,不論是地板上的抽屜、櫥櫃裡的抽屜、櫥櫃本身的邊邊,這些平行線在三維空間中通通都平行於地面。因此這些平行線的消失點會落在照片上同一條水平線上。
換句話說,要是該平行線組並沒有平行於地面,那麼他的消失點就不會落在該線上。舉例來說像下圖,V1和V2這兩個消失點會在同一條水平線��上,是因為空間中朝向V1, V2方向的平行線平行於地面。而斜屋頂的消失點V3因為不平行於地面,所以消失點不會在V1和V2的連線上。
那為什麼V3, V1, V4會在同一條線上呢? 因為這些的平行線雖然方向不同,但都平行於該房子的左面,所以他們的消失點會落在同一條線上。
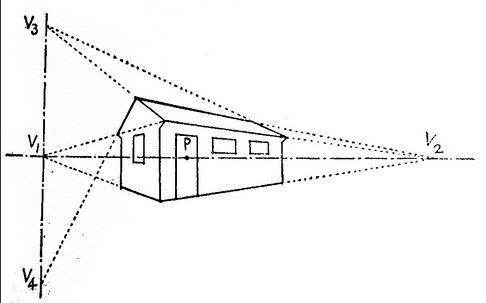
圖片出自HSUEH Gallery
一點透視是個假議題
想通了這一點後,你會發現,大家平常在說的一點透視、二點透視、三點透視,通通都是假議題。 所謂的一點透視,只是剛好圖片適合用一組最有代表性的平行方向來畫
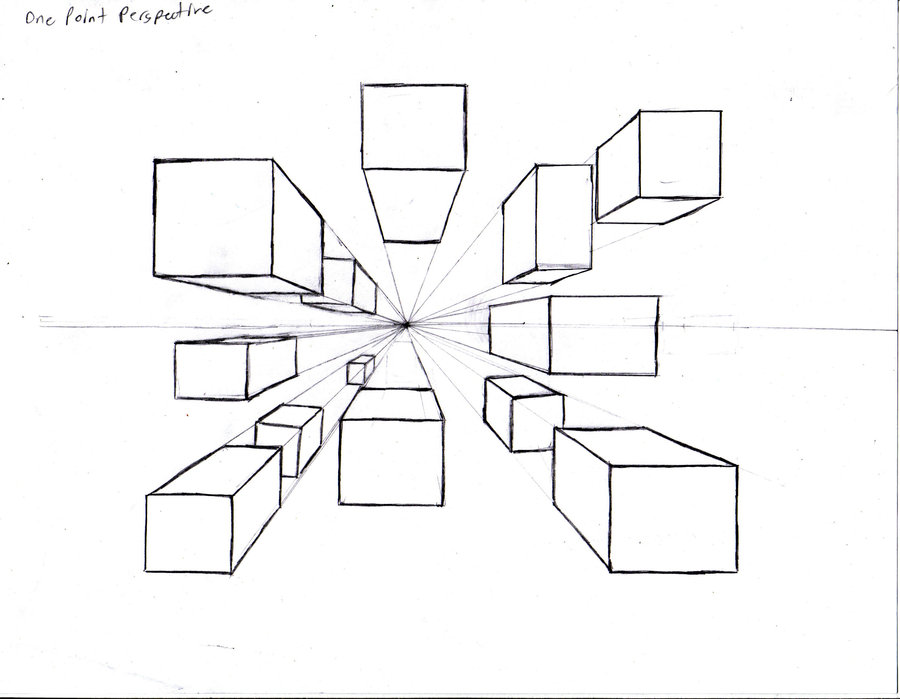
圖片出自GCS ARTS
兩點透視,只是剛好圖片適合用兩組最有代表性的平行方向來畫
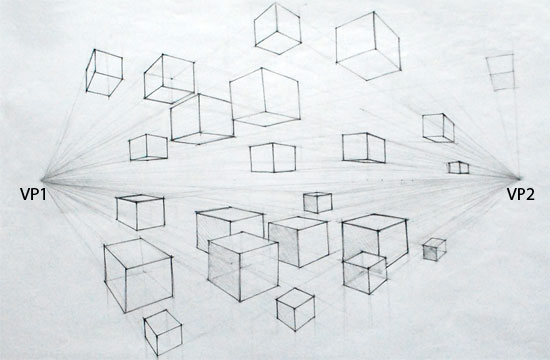
圖片出自D'source
三點透視 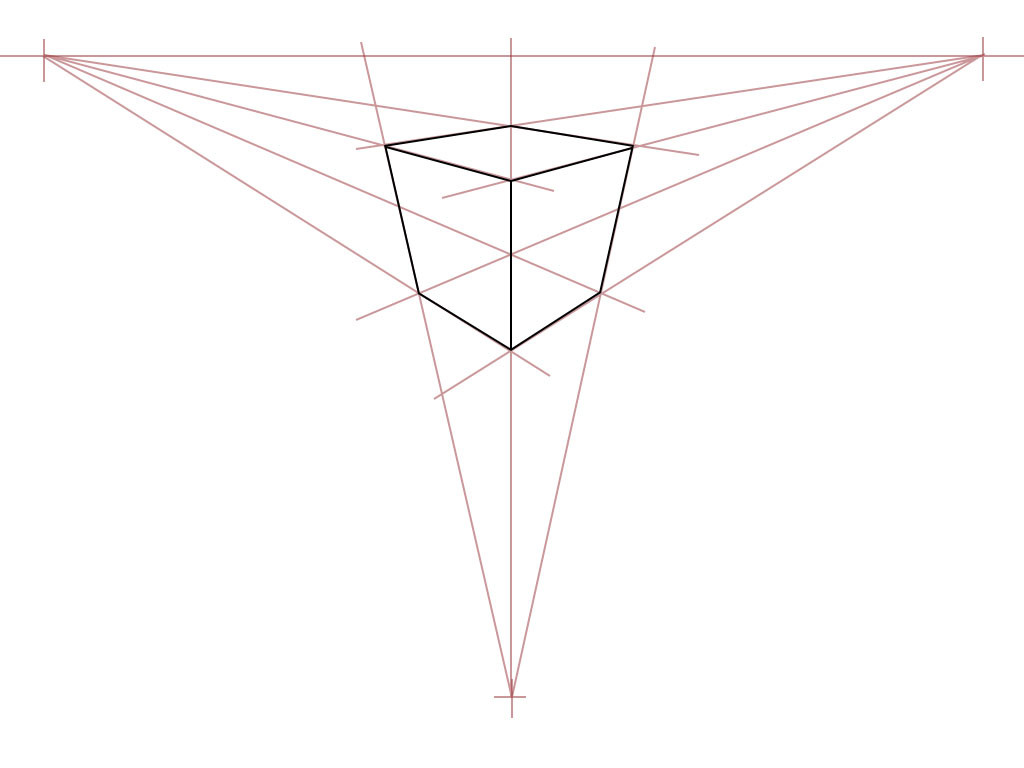
思考的關鍵在於,你的投影中心、投影平面,和整個三維世界的連線。只要記得大原則「所有同樣方向平行線的無限遠處,會落在投影平面上的同一點」,其他就可以一一推導出來。
網路上大部分談透視的文章都是繪畫類型的,用作畫的角度來看透視,另外一小部份是計算機圖學的類型,用矩陣和齊次座標系來看透視。要用簡單的方式把透視的觀念講清楚,我覺得不是件很容易的事情,昨天把這個想法告訴朋友,他們都有種醍醐灌頂的感覺,故寫成文章以茲紀念。